跳至主要內容

线代

fakeppa2025年9月11日大约 4 分钟归档

一生之敌--线代

矩阵的运算法则

image.png
image.png
    1. 本行作为被减数，减去其他行的k倍，保持矩阵的基本性质，可以进行运算（对应行列式2，相）
    1. 交换任意两行，也是可以进行的操作（对应行列式3，不同）
    1. 某行直接乘k，不改变矩阵性质（对应行列式1，不同）

行列式运算法则

image.png
行列式，顾名思义行和列都可以进行操作

    1. 行和列要乘k，必须先把k提到行列式外面
    1. 本行作为被减数，减去其他行的k倍，与原行列式相等，可以进行运算，这也是与矩阵相同的地方
    1. 要交换行或者列，必须改变符号

技巧--求秩

1. 向量组求秩

求秩最简单的应用----求秩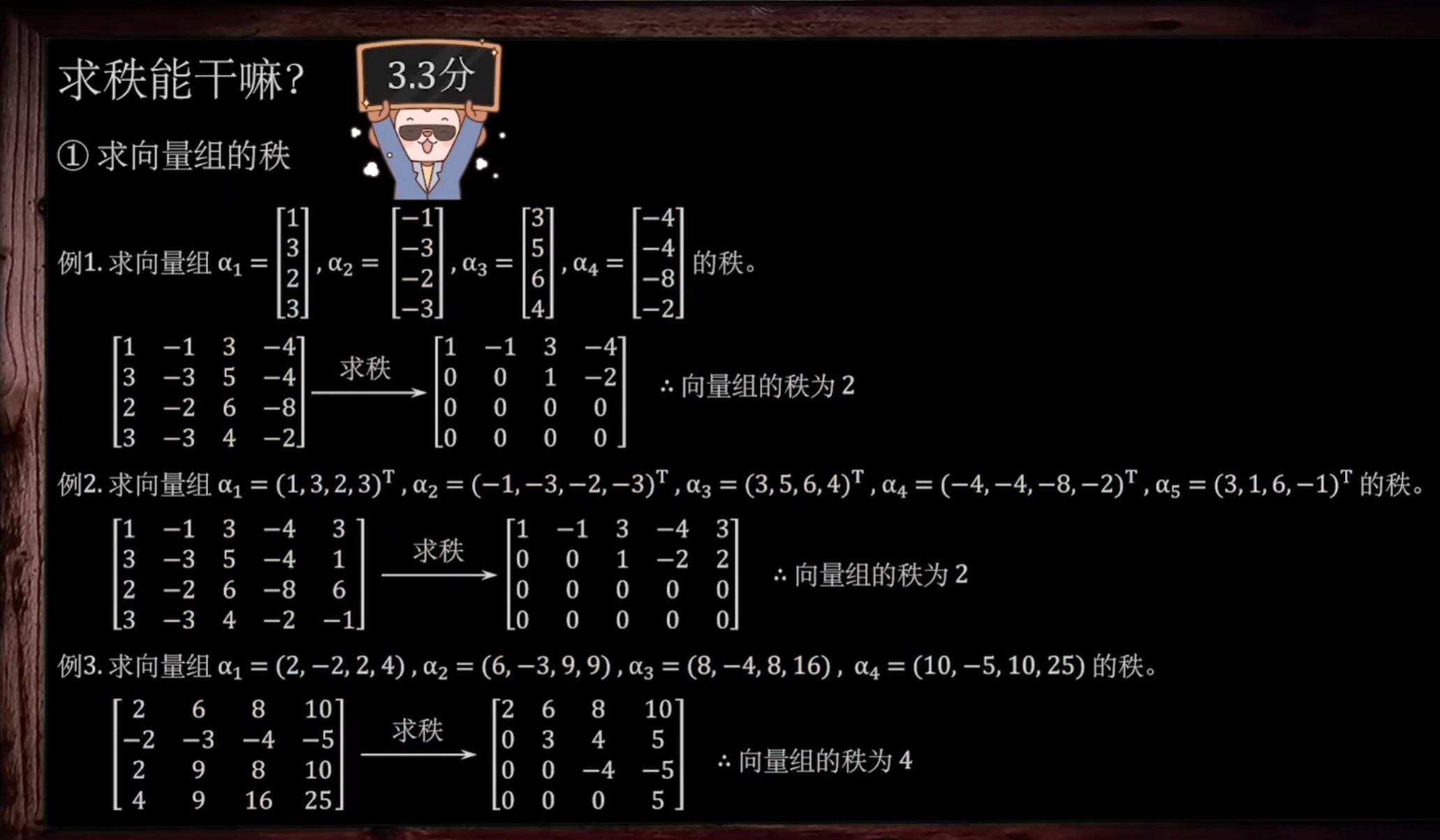
image.png

2. 判断线性相关性

小弟大哥是什么？
image.png

image.png
image.png

3. 判断！能否能线性表示

知识点：线性相关性

  1. 把这些向量组合起来求解秩
  2. 然后把题干给出的向量组和，再次求解秩
  3. 若秩等于原向量组，则此向量可以由向量组线性表示
  4. 若秩不等于原向量组，则此向量不可以由向量组线性表示
    image.png

4. 求最大无关组（不求通解特解版）

关注列！注意最大无关组只求秩即可
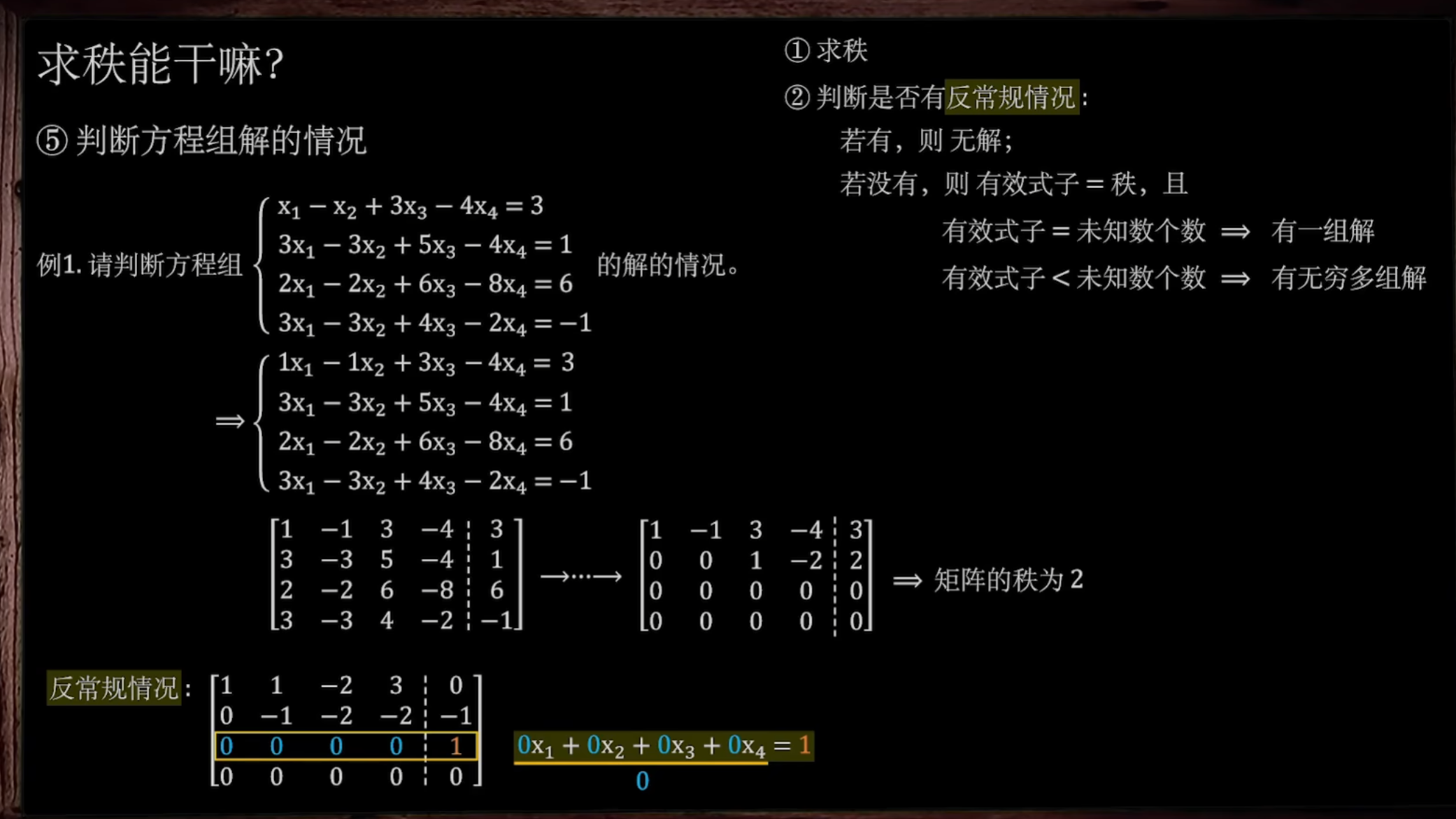
image.png
例题
image.png

5. 求方程组的解的个数

判断是否常规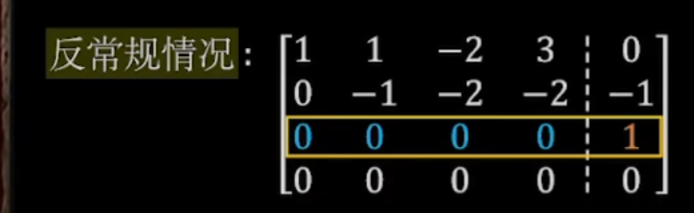
image.png
本题的1在等号右侧，意味着秩<1
image.png

image.png
image.png

求最简型矩阵能干嘛？

1. 极大无关组表示向量

注意，为什么这个比之前求极大无关组多了个求行最简而不是行阶梯？
因为这题要求的用极大无关组表示其余向量，其余向量需要行最简行形式体现~！而最大无关组根本不用表示！

  1. 化成行最简形式，然后看横看行最简，竖直方向的向量，那个就是极大无关组
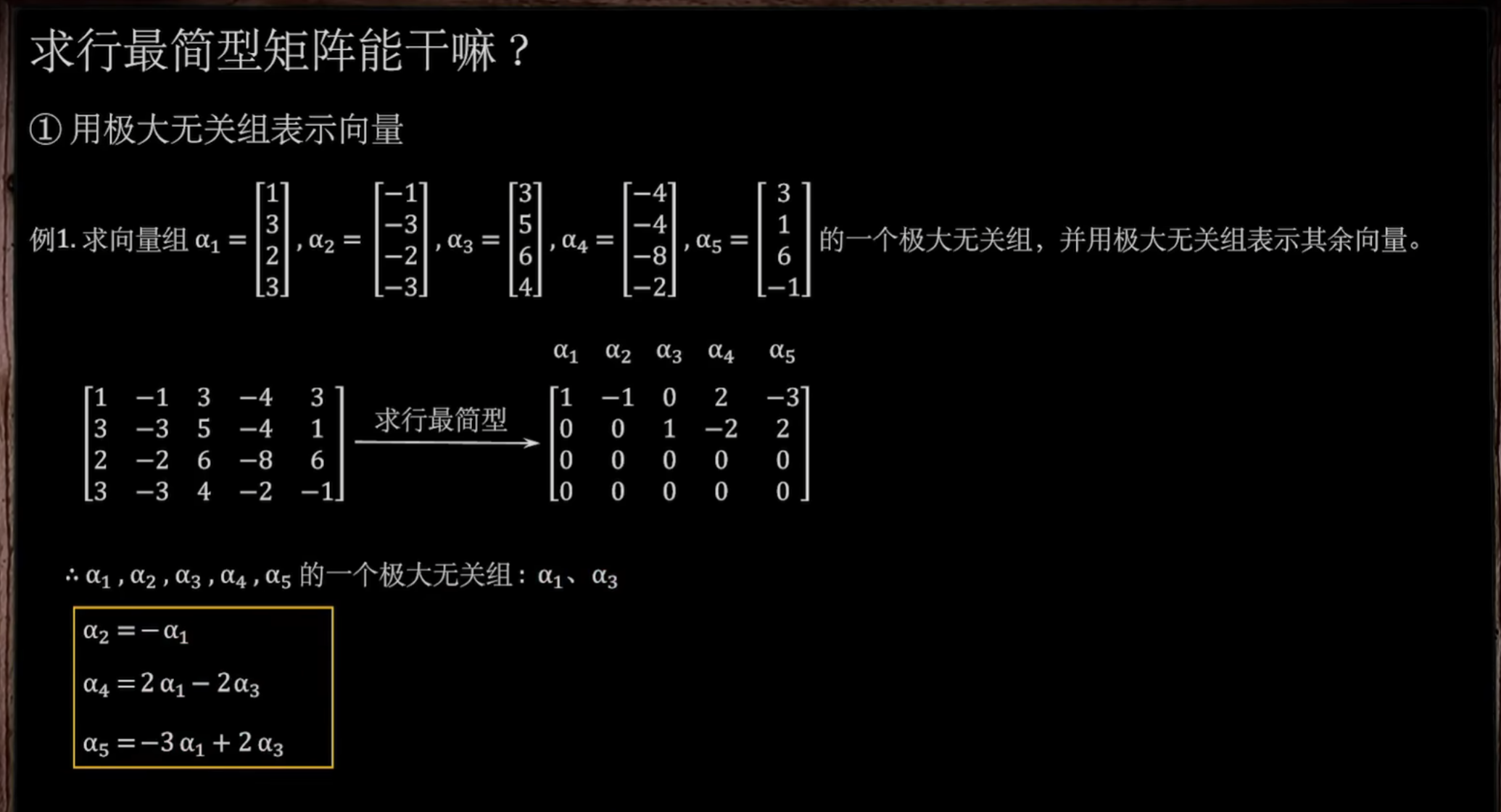
    image.png
  2. 求其余向量，几乎可以不动脑子，我们横着列出所有的其他向量，然后把极大无关组向量竖着乘进去（不用展开极大无关组），化简可以得到向量的形式
    image.png

2. 求方程的通解和特解

  1. 先化成行最简型
  2. 然后立即用方程组的形式运算（因为需要记录数在哪一列，在那列就是x几，注意常数列！）
  3. 把每行最左边的数放到等号左边，其余放到右边
  4. 然后发现可能缺一些x，将它们补齐，只需要补充x几等于x几即可
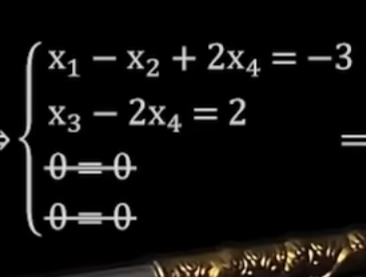
    image.png
  5. 重要的易混淆来了，我们在右侧补充的x几是跟之前化简出来的行最简有关系的，不能补充行最简的那个纵向！！！
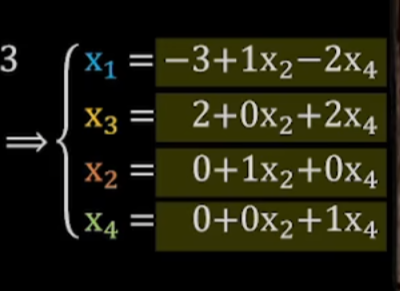
    image.png
    最后我们把这个方程组"切西瓜"，最终答案是下图的x2和x4换成k2和k4即可
    image.png
    如果要求特解的话，只需要把其中的k1和k2赋值0即可
    image.png

3. 求行最简型矩阵

不多说，最简单
image.png

行列式会求，能干什么

1. 判断 “矩阵” 是否可逆，方法:

image.png
image.png

例题：
image.png

2. 求矩阵特征值

image.png
注意：行列式算出的特征值的个数必须等于行列式的行数！！！
例题
![image.png](https://cdn.jsdelivr.net/gh/fakeppa/ blog-img/20250915001611.png)

综合题目

1. 求特征向量

涉及知识点：求通解，求特征值

k1与k2不能全取0！
image.png
解题过程
image.png

求对角矩阵和可逆矩阵

知识点：特征值、特征向量
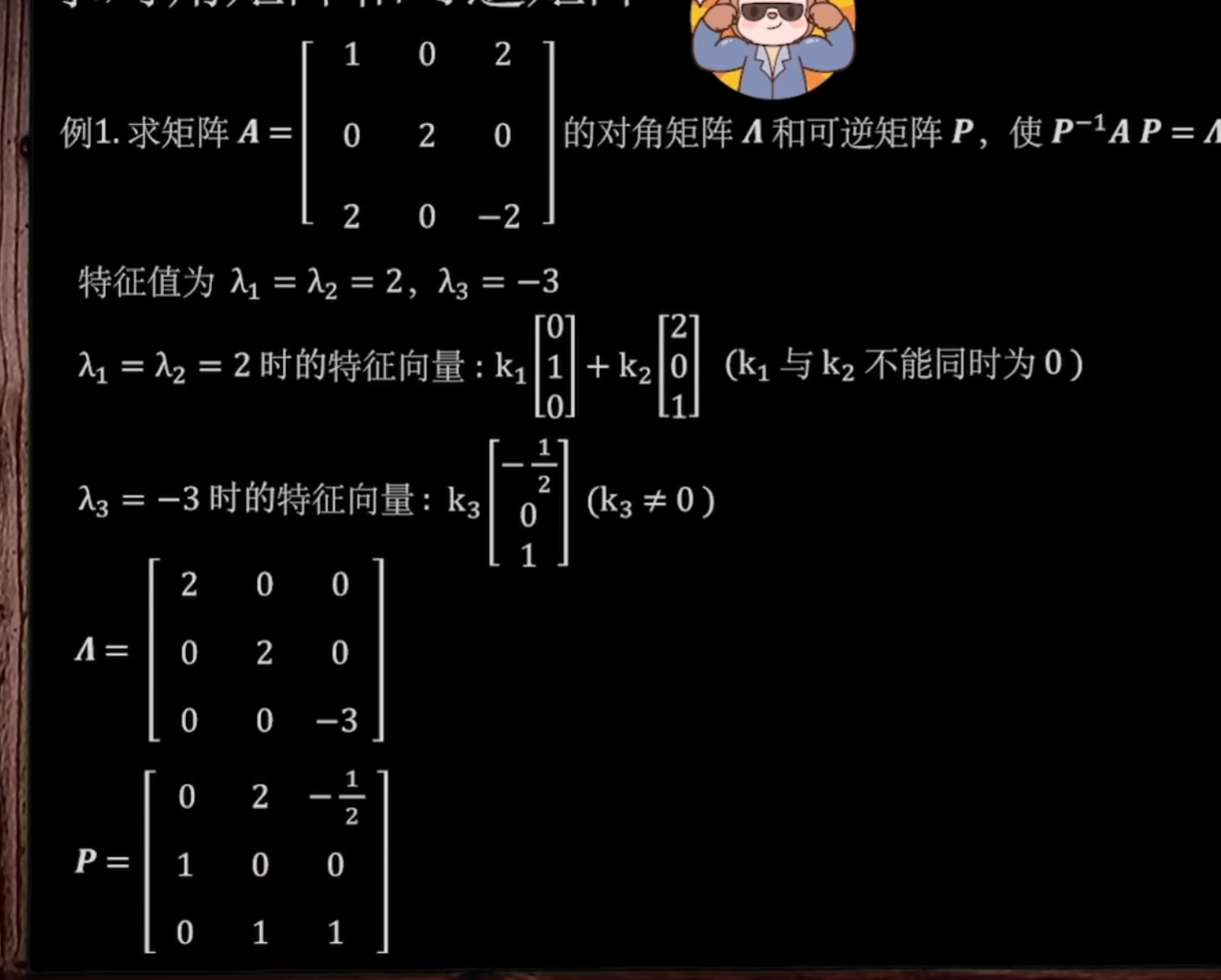
image.png

解题过程
image.png

求对角矩阵和正交矩阵

知识点：特征值和特征向量
稍麻烦一些
image.png

求二次型的标准型和正交矩阵

前置知识：求二次型f的矩阵A

image.png
对应系数分配
image.png

方法

image.png
image.png
到底了:D
Copyright © 2025 fakeppa