高数下

大串讲

二元函数极限

存在问题

可以快速判断比值形式得极限是否存在，特殊情况可以判断极限大小

多元函数极值

极值判定

分两步，第一步关键，第二部验证（充分性的来源）

求极值

再极值判定之前求驻点即可，可能有多个驻点，用判定法判定即可

题目

求极值

空间直线，平面相交问题

已知直线和平面，求投影直线方程

直接套流程

1. 直线方向向量叉乘平面法向量，得出投影面（投影面是必然垂直于平面的且包含直线）的法向量
   不同的直线形式的方向向量求法不同，这也算是一个考点
   对称式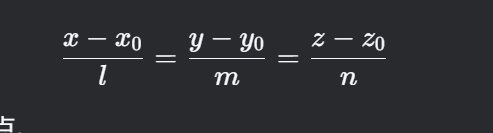
   

• 方向向量求法
  直接读广泛参数
  参数式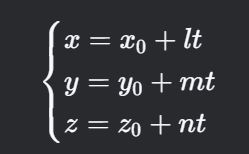
  
• 方向向量求法：
  • 直接读取参数 t 的系数！
  • d⃗=(l,m,n)d=(l,m,n)
    一般式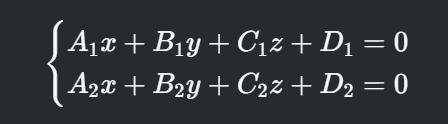
    
• 方向向量求法
  联立叉乘

1. 联立投影面方程和平面方程，求出直线方程

直线过点平行于平面，与直线相交求直线方程问题

image.png

1. 求出过点与平面平行的平面方程
2. （重点）求平面方程与目标直线的交点，利用参数方程，与对称式互化，注意到参数式的特性，可以知道直线上的一个点，那么直接带入平面方程，即可求出参数大小---即知道点的坐标！
3. 第二步求得的点与题给点联立即可求出直线方程

求给定函数、给定点、给定方向向量，求方向导数

1. 先求函数对x、y的偏导

2. 所求点的坐标带入偏导x、y式子

3. 求给定方向的方向余弦

   • 向量单位化
   • 
     image.png

4. 套公式
   用第二步的对x偏导乘cosa，加上，对y偏导乘cosb即可

二重积分

第六题题型

积分换序问题

换序，即将图像换一个方向观察

• 1. 先按照原积分上下限确定图形形状，图形范围，注意外层上下限为内层上下限的“定义域”，所以要带入内层上下限的函数得出图像上写出的数值
• 2. 再重新写出内层的换方向看的积分的函数，并按照此方向，确定范围，写入外层积分即可
     

对称性问题

解题步骤

• 1. 各个范围首先做出上下限图形
• 2. 判断图形形状是否关于x轴或y轴对称，抓住对称部分
• 3. 按照被积函数的奇偶性，并同时依据关于哪个轴对称，就对哪个未知数视为自变量，判断奇偶性。
  • 若为奇函数，则直接为0。
  • 若为偶函数，则直接为2倍的此积分上下限区间
    

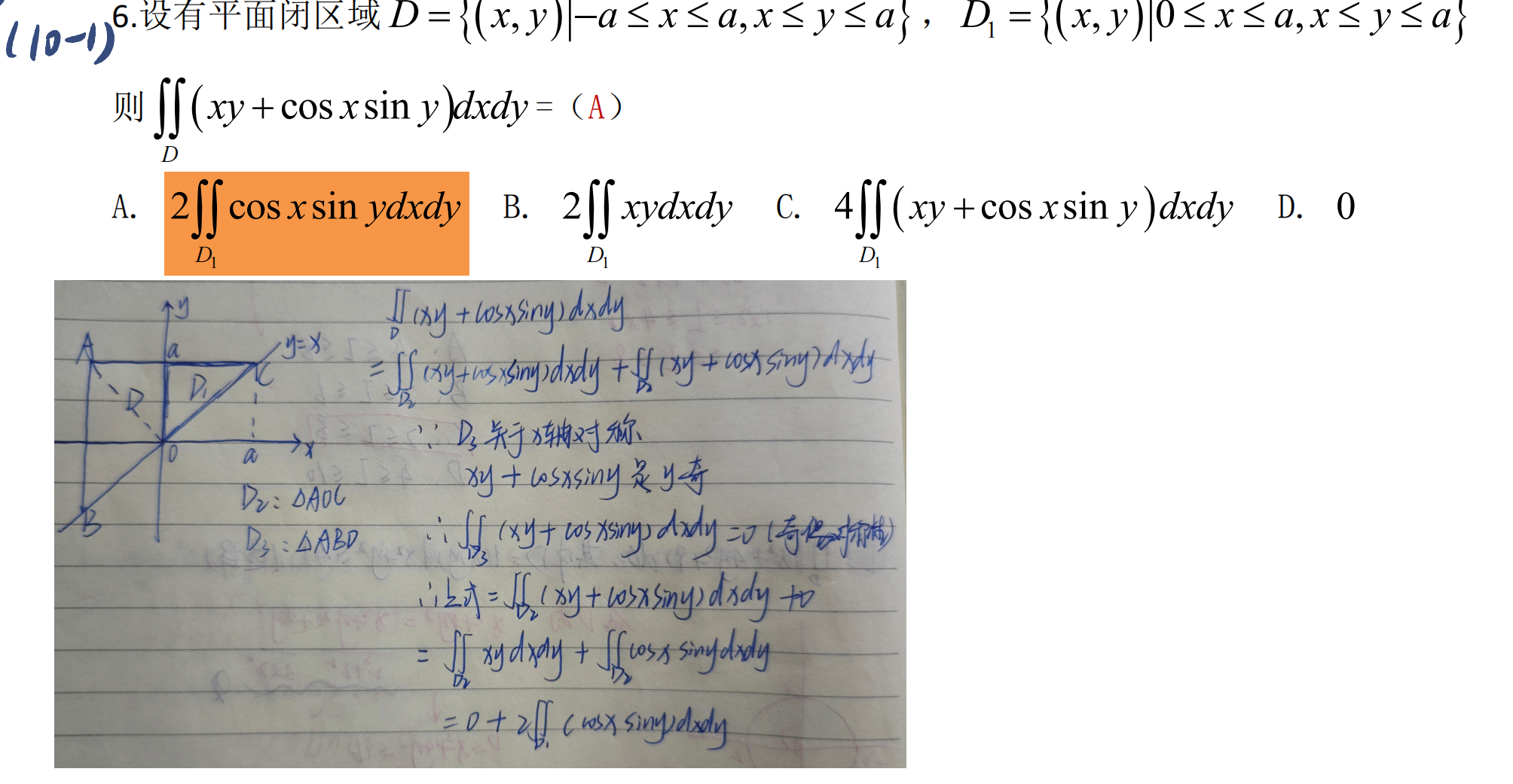
特解题

按照二重积分的性质计算
性质1包含两个部分，一方面揭示了常数可以直接提前，另一方面主要表达了+号多项式可以分为两个积分表达式

• 先按照性质1，直接将常数提出
• 随后按照性质3，把积分式转化为面积问题，用圆面积公式解答
  

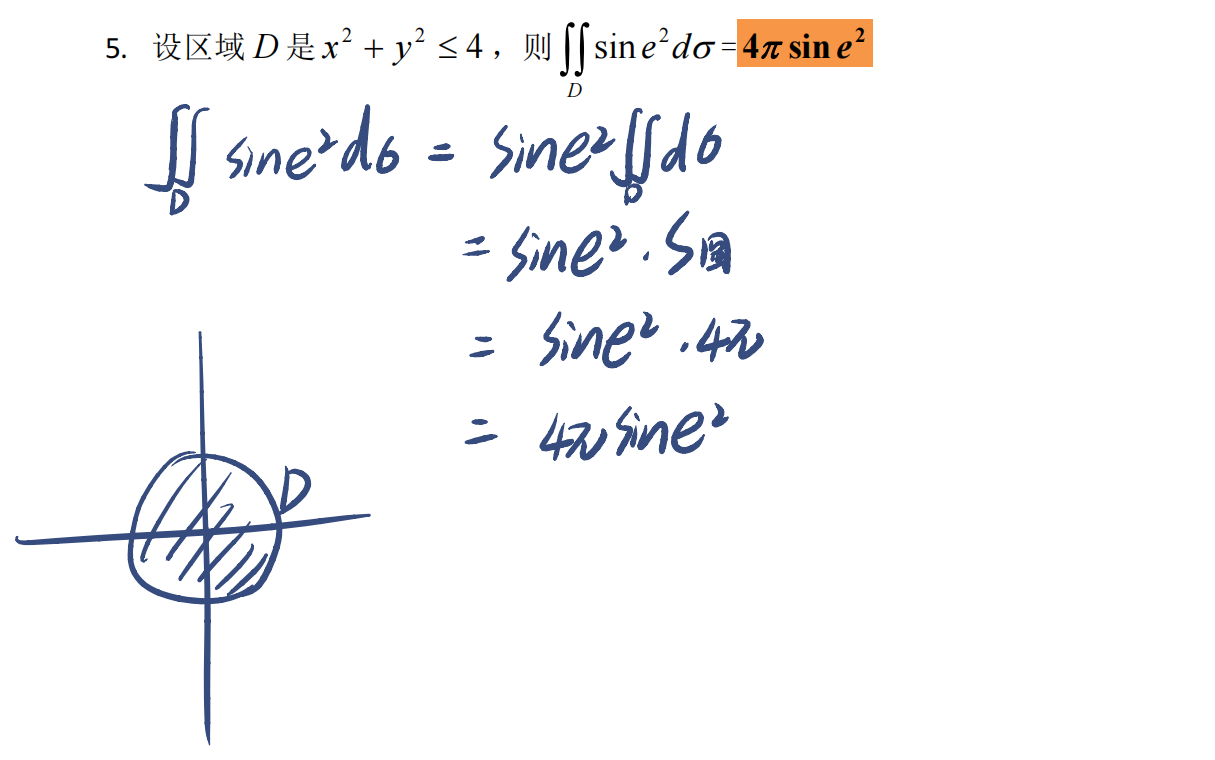
极坐标

华里士公式：点火公式，sin和cos的积分相等，然后倒计时就是得数

极坐标公式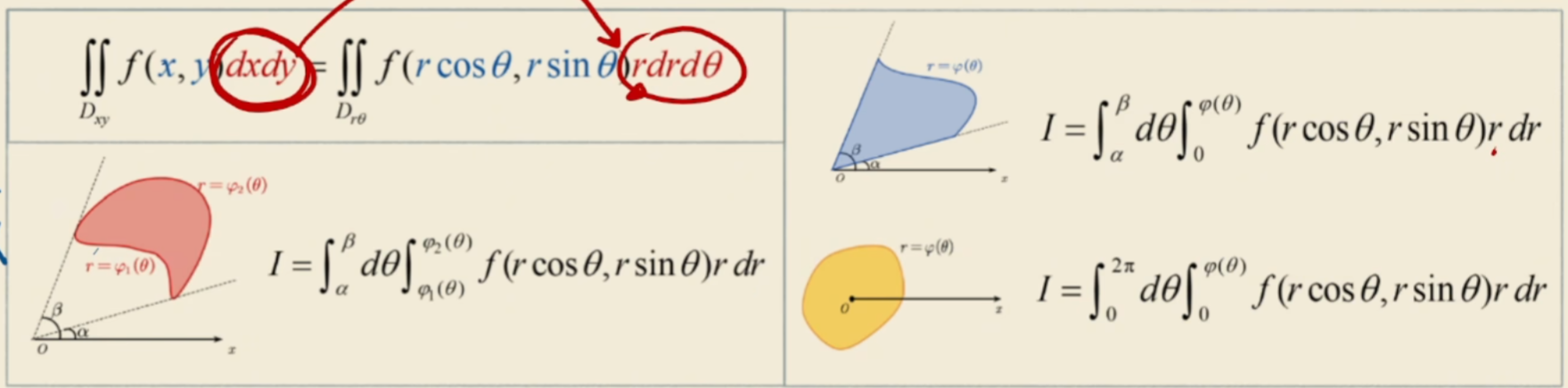

极坐标左边的积分上下限是角度，右边的上下限分别是从原点出发的射线穿过的最小长度和最大长度，按照x=rcos&，y=rsin&计算

题目

注意右下角红色字体，能够留下角度值！！！

求体积

极坐标+空间解析几何+二重积分体积公式
⚠️upload failed, check dev console

1. 先求出积分区间D：
   先联立两个曲面，消掉Z，用（极坐标）r=x^2+y2的公式带入解出带半径
2. 再带入曲面：上曲面函数-下曲面函数进行二重积分
3. 极坐标换元解出答案

弧长公式