数据结构
考纲
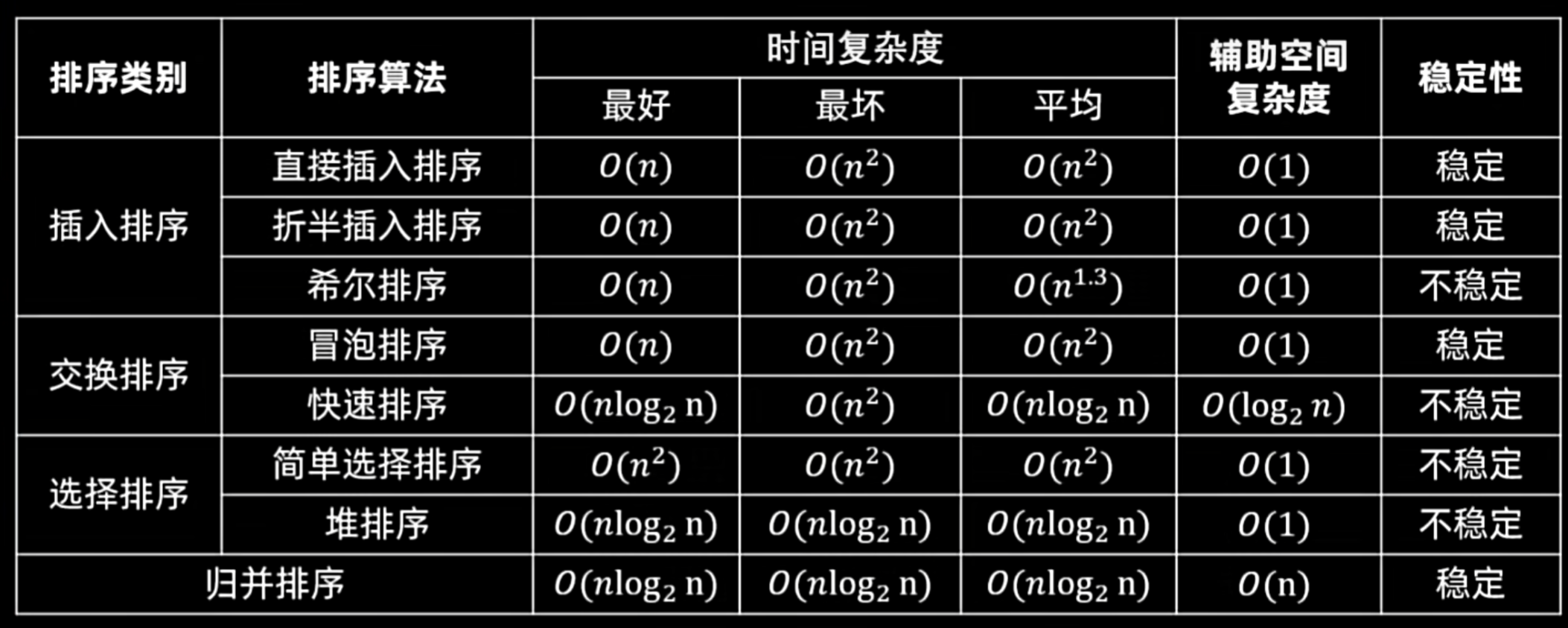
题型分类
章节
核心考点/题型说明
**大题 (重点)**
第七章 树
- 二叉树遍历(先/中/后序)
- 线索二叉树
- 哈夫曼树与编码(画树、写编码)
- 树的性质计算
第八章 图
- 图的遍历(深度优先DFS、广度优先BFS)
- 最小生成树(Prim算法, Kruskal算法)
- 最短路径(Dijkstra算法,必考)
- 图的存储结构
第九章 查找
- 二叉排序树(构建、插入、删除等)
- 平衡二叉树(了解概念)
- 哈希表(冲突处理)
**程序题 (代码)**
第九章 查找
程序填空/选择大题:
- 顺序查找
- 折半查找
第十章 排序
程序填空/选择大题:
- 直接插入排序
- 折半插入排序
**小题 (概念/基础)**
第一章 绪论
选择题:基本概念、定义
第二章 线性表
小题:顺序表、单链表、链表、线性表的相关基础操作与概念
第三章 栈和队列
小题:栈与队列的基本特性、操作
第八章 图
小题:AOE网的相关概
念
树结构的线性存储
1. 顺序存储法(二叉树逻辑较简单)
根据二叉树的顺序存储规则,根节点存储在索引1(或0),对于任意节点 i,其左子节点存储在 2i 处,右子节点存储在 2i+1 处(若从0开始索引,则左子节点为 2i+1,右子节点为 2i+2)。空缺位置用0表示。
2. 链式存储法(主流方法)
存储表(数组实现)
| 索引 | 数据 | 父节点索引 |
|---|---|---|
| 0 | A | -1 |
| 1 | B | 0 |
| 2 | C | 0 |
| 3 | D | 0 |
| 4 | E | 1 |
| 5 | F | 2 |
| 6 | H | 3 |
| 优点:找父亲、找根极快。 | ||
| 缺点:找所有孩子极慢(需遍历整个表)。 |
写做: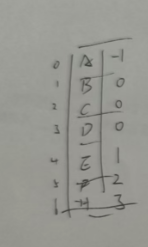
2. 孩子表示法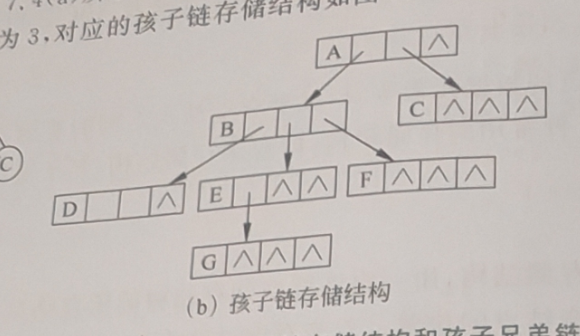
每个节点记录“所有孩子是谁”。
节点数组(顺序表):
| 索引 | 数据 | 第一个孩子指针 |
|---|---|---|
| 0 | A | → [1] → [2] → [3] → NULL |
| 1 | B | → [4] → NULL |
| 2 | C | → [5] → NULL |
| 3 | D | → [6] → NULL |
| 4 | E | NULL |
| 5 | F | NULL |
| 6 | H | NULL |
3. 孩子兄弟表示法(最常用、最重要)
这是将任意树转换为二叉树的标准方法。每个节点包含
数据firstChild:指向第一个孩子nextSibling:指向下一个兄弟
写做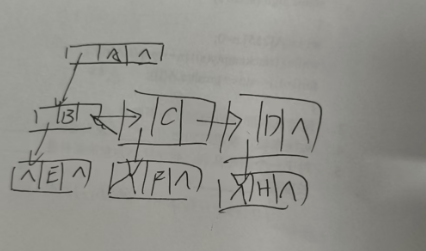
方法三:其他与高级方法
1. 边表表示法(适用于以边为核心的操作)
存储所有边(如(A,B), (A,C), (A,D), (B,E), (C,F), (D,H)),再配合节点表。在图论中更常见。
2. 邻接表(图的通用表示,树是特殊的图)
与“孩子表示法”类似,是图的标准存储方式之一,每个节点维护一个邻居(孩子)链表。
3. 线索二叉树(您之前问到的——这是方法的“优化”,而非独立方法)
它建立在孩子兄弟表示法(二叉链表) 之上。通过在空指针域中存储遍历顺序下的前驱/后继(称为“线索”),来加速遍历操作。其底层物理结构依然是二叉链表。
线索二叉树--二叉链表与双链表的结合
// 线索二叉树节点结构
typedef struct ThreadNode {
ElemType data;
struct ThreadNode *lchild, *rchild;
int ltag; // 0:指向孩子,1:指向前驱线索
int rtag; // 0:指向孩子,1:指向后继线索
} ThreadNode;中序线索化
将二叉树转为孩子表示法,再中序遍历,将中序遍历结果作为线索
空闲的标志位在1时,前驱表示中序遍历的前驱,后继表示为中序遍历的后继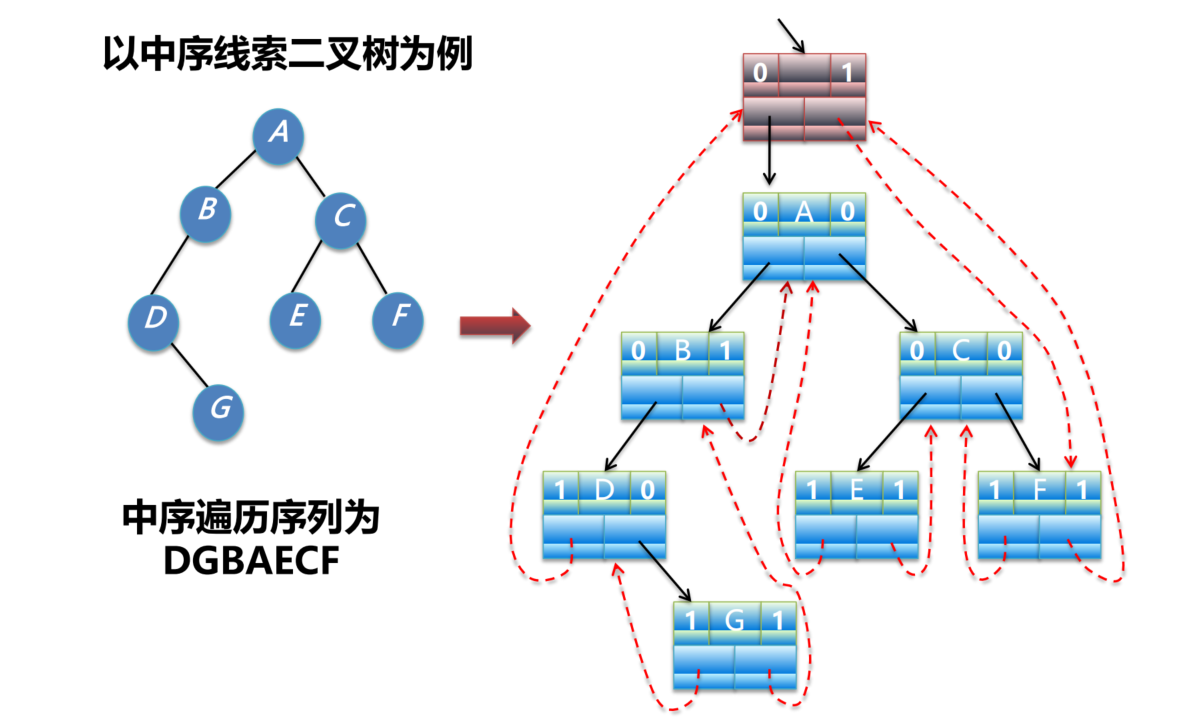
关于中序第一个节点的线索和最后一个节点的线索问题
无头节点
第一个元素的左指针若空闲指向NULL,最后一个元素右指针若空闲也指向NULL
有头节点
头节点的左指针指向第一个元素,右指针指向最后一个元素,而第一个元素指向头节点,最后一个元素指向头节点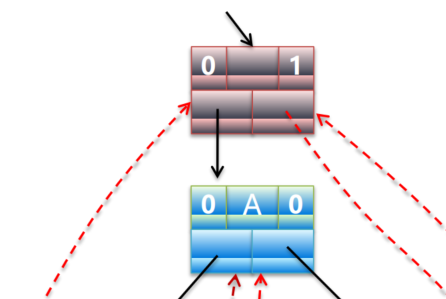
最小生成树算法(无向图)
目标:生成的树边权和一定唯一,生成树不唯一
加点法----普利姆算法
从任一顶点开始,每次选择连接已选顶点集和未选顶点集的最小权边,将该边及其连接的未选顶点加入生成树,直到所有顶点都被选中
加边法----克鲁斯卡尔算法
将所有边按权值从小到大排序,依次选择每条边,若该边连接的两个顶点不在同一连通分量中,则加入该边,否则跳过,直到选中 n-1 条边(n 为顶点数)
折半查找
要求:1.必须是数组(顺序表)2.数据必须是有顺序的
- 指定left和right指针,left指向首个元素,right指向最后一个元素,表明数组的范围
- mid指向数组的中间位置((left+right)/2),将我的数字与mid指向的数据进行比较
- 如果数字比我的大,则缩小right到mid-1的位置.如果数字比我的小,则扩大left到m id+1的位置
- 重复步骤2和4,缩小到最后,出现小数点,向下取整,然后再进行比较
- 如果left大于right,就是找不到了
总复习
第一优先级(重中之重,必须掌握)
目标:掌握这些内容,就能解决绝大部分大题和核心程序题。
第八章 图
最短路径:Dijkstra算法(考纲明确“必考”)。必须能逐步推演、写出过程。
画一个表,选定一个点,从此点开始,寻找到每个结点的权值最小值,填入对应轮次的表格内,不可达填写∞,并在当前轮次选择一个最小权值的点,作为确定值,以后不再对此值进行改变,并作为下一轮次的初始结点,寻找到每个结点的权值最小值。图的遍历:深度优先搜索(DFS)和广度优先搜索(BFS)的序列结果。
如果给邻接表,则只有唯一解,按照邻接表的顺序,进行深度、广度遍历,最后输出序列结果最小生成树:Prim算法和Kruskal算法的步骤、区别及应用场景。
我了解了Prim算法和Kruskal算法,不了解区别以及应用场景具体如下:
Prim先选中图中任意结点,然后再查找最近路径且通向未选中过的结点,选中后继续查找最近路径且通向未选中过的结点,以此类推,直到选中所有点
Kruskal算法先只关注所有点,在点之间选择权值最小的路径,且这个路径不在一个连通集合内,直到连接所有的点,没有未连接的连通变量
第七章 树
二叉树遍历:给定一棵树,能写出先序、中序、后序遍历序列(大题基础)。
先序先访问当前,然后递归访问左子树,右子树
中序先递归访问左子树,然后访问当前,递归访问右子树
后序先递归访问左子树,递归访问右子树,最后访问当前结点哈夫曼树与编码:能根据一组权值画出哈夫曼树,并写出对应的哈夫曼编码。
先将一组权值对应的数据从小到大排序,选出两个最小权值,相加获得其父的权值大小,然后划去已经构造进树的权值,将其相加获得的权值做个标记,加入到升序的权值表中,然后再进行之前的步骤,如果在权值升序列表中遇到构造出来的父节点(做标记过的权值),则将其顺序下一个元素与其构成兄弟,算出父节点的权值,继续添加到权值升序表内,知道所有的权值元素都已经构造进树内,这就是一颗哈夫曼树
在哈夫曼树的根节点向下遍历访问,左子树为编码0,右子树为编码1
第九章 查找
- 二叉排序树:给定一个序列,能画出二叉排序树的构造过程,以及插入、删除结点的操作。
将序列中的任意结点作为根节点,选择第一个元素,如果比根节点小则想左构造子树,反之向右,对于目标结点的构造需要对根节点左右两颗子树进行递归比较
实现插入,则将此数值用二叉排序树进行递归比较构造即可
实现删除,如果删除的结点只有左子树或者右子树,则之间删除这个结点,让其子树代替他即可,如果选择删除的点有左右两个子树,那么,递归以下算法,选择其左子树中最大的结点,代替目标结点,然后对替代结点进行递归删除
- 二叉排序树:给定一个序列,能画出二叉排序树的构造过程,以及插入、删除结点的操作。
🥈 第二优先级(重要得分点,需熟练)
目标:这些是程序大题和重要概念的核心,需理解透彻。
第九章 查找 & 第十章 排序
- 程序填空题/选择题:重点理解折半查找、直接插入排序、折半插入排序的算法逻辑、代码流程和边界条件。动手模拟代码执行。
折半查找
int left=0;
int right=arr.length()-1; // ❌ 错误1: 数组长度是属性,不是方法
int mid;
while (!(left>right)){ // ✅ 正确但建议用 left <= right
mid = (right+left)/2;
if (target>arr[mid]){
left=mid+1;
}
else if(target<arrp[mid]){ // ❌ 错误2: 数组名拼写错误(arrp)
right=mid-1;
}
else{
retern mid; // ❌ 错误3: 拼写错误(return)
}
}
return False // ❌ 错误4: 类型不匹配(应返回int)int left=0;
int right=arr.length-1;
int mid;
while (left<=right){
mid = (right+left)/2;
if (target>arr[mid]){
left=mid+1;
}
else if(target<arr[mid]){
right=mid-1;
}
else{
return mid;
}
}
return -1直接插入排序
int temp = 0; // ❌ 错误1: temp应为arr[i],不是0
int complete=0 // ✅
while (complete==arr.length-1){// ❌ 错误2: 循环条件应为complete<arr.length-1
arr[complete+1]=temp; // ❌ 错误3: 赋值反了(应为temp=arr[complete+1])
for(int i=0;i<arr.length-1;i++){// ❌ 错误4: 不应遍历整个数组
if(temp<arr.[i]){ // ❌ 错误5: 多了一个点(arr.)
for(int n =i;n--;n==0){ // ❌ 错误6: 循环语法错误
arr[n+1]=arr[n]; // ❌ 错误7: 移动逻辑混乱
}
arr[complete]=temp; // ❌ 错误8: 插入位置错误
}
}
complete+=1;
}for (int i = 1; i < arr.length; i++) { // 从第2个元素开始
int temp = arr[i]; // 待插入元素
int j = i - 1;
// 向后移动大于temp的元素
while (j >= 0 && arr[j] > temp) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = temp; // 插入到正确位置
}折半插入排序
int temp = 0;
int complete=0;
int left=0;
int right=arr.length()-1; // ❌ 错误1: 应为right=complete,不是整个数组
int mid;
while (complete!=arr.length/2){ // ❌ 错误2: 循环条件错误
arr[complete+1]=temp; // ❌ 错误3: 同直接插入
// ... 此处重复了直接插入的代码,逻辑混乱
while (complete==arr.length-1){ // ❌ 错误4: 死循环条件
arr[complete+1]=temp;
while (!(left>right)){
mid = (right+left)/2;
if (temp>arr[mid]){
left=mid+1;
}
else if(target<arrp[mid]){ // ❌ 错误5: 变量名错误(target)
right=mid-1;
}
}
for(int n =i;n--;n==0){ // ❌ 错误6: 变量i未定义
arr[n+1]=arr[n];
}
arr[left]=temp // ❌ 错误7: 缺少分号
complete+=1;
}for (int i = 1; i < arr.length; i++) {
int temp = arr[i];
int left = 0;
int right = i - 1; // 只在已排序部分查找
// 折半查找插入位置
while (left <= right) {
int mid = (left + right) / 2;
if (arr[mid] < temp) {
left = mid + 1;
} else {
right = mid - 1;
}
}
// 移动元素
for (int j = i - 1; j >= left; j--) {
arr[j + 1] = arr[j];
}
// 插入
arr[left] = temp;
}第七章 树 & 第九章 查找
线索二叉树:理解线索化的目的,能进行线索化。
半懂
哈希表:掌握处理哈希冲突的几种主要方法(如开放定址法、链地址法)。
开放定址法是线性探测法吗,那个会,拉链法也掌握了
🥉 第三优先级(基础保障,需熟记)
目标:确保小题和概念题不丢分。
第一章 绪论:数据结构的基本概念、术语定义。
第二章 线性表:顺序表和链表(单链表)的基本操作、特点、区别。
第三章 栈和队列:栈(FILO)和队列(FIFO)的特性、基本操作。
第八章 图:
图的存储结构(邻接矩阵、邻接表)。
AOE网的相关概念(如关键路径)。
