跳至主要內容

统概

fakeppa2025年11月19日大约 6 分钟归档

全概率与贝叶斯公式

EZ
跳过，若有难题后看

技巧

求至少一个存在的概率：加奇减偶
image.png

离散型

例1

image.png
取值和概率离散相关
（2）所有概率加一起为1
（3）将x列平方，并将平方后相等的内容合并
（4）期望：x对应数值乘P对应数值
DX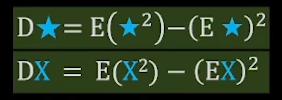：image.png

例2

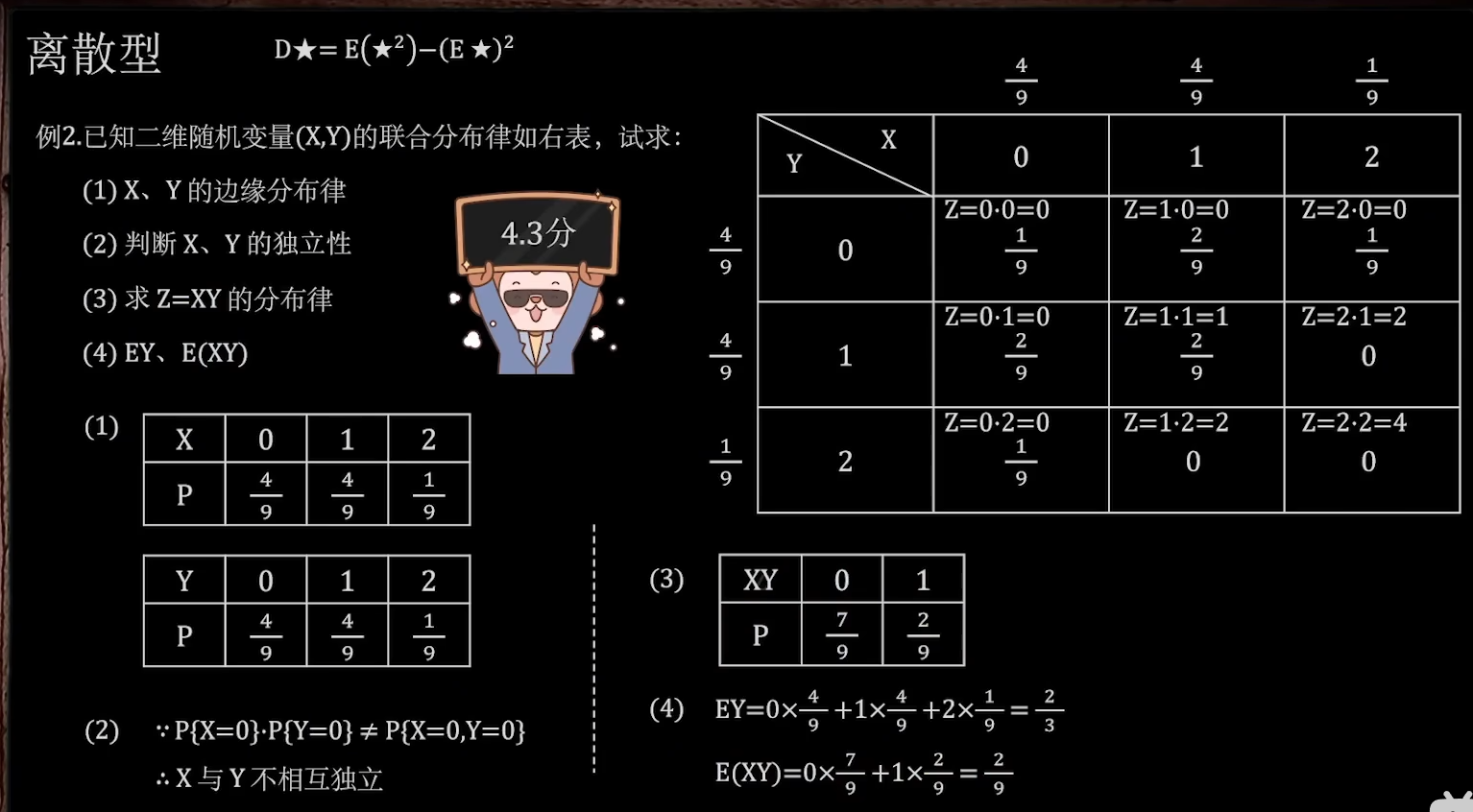
image.png
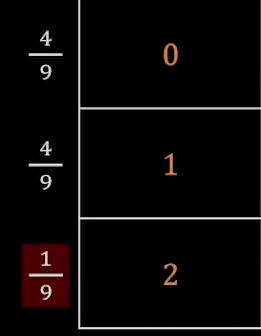
image.png

（1）边缘分布律：image.png
每列各数相加，image.png
每行各数相加，image.png
获得了两个1维小表就是x和y的边缘分布律：image.png

（2）判断独立性的方法：
在二维表中， 选取数字，x和y相乘，是否等于 这个数字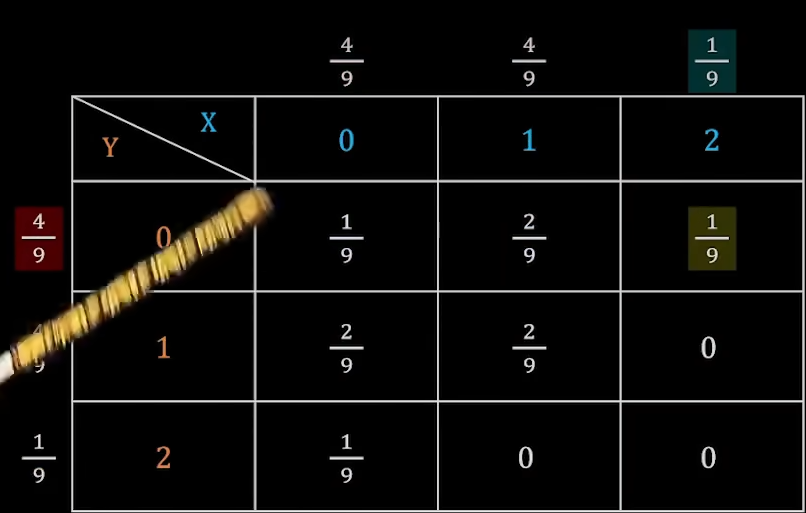image.png
具体写法image.png
（3）求z=xy的分布律：
就是将x数值和y数值相乘，整合成一维表即可

一维连续型

公式1

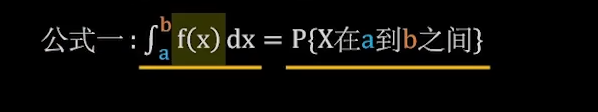
image.png
image.png

例题1

image.png
积分结果就是需要求的概率：

推论1：

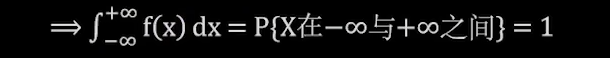
image.png
image.png

例题2

特征：密度函数！！！！！！！！！且求的是未知数
image.png
如果是分布函数F(x)只需要求区间端点相等即可！！！！！！！！

公式2

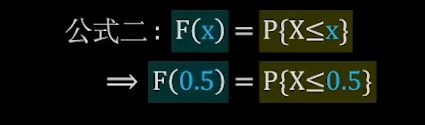
image.png
image.png

例题3

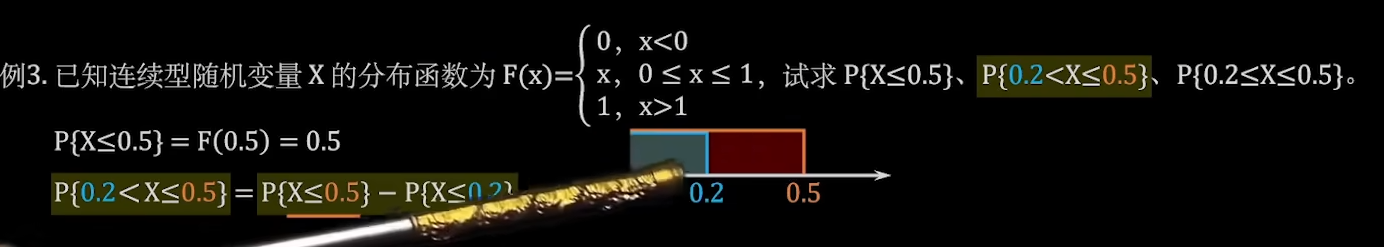
image.png
小于等于需要加上等于此值得概率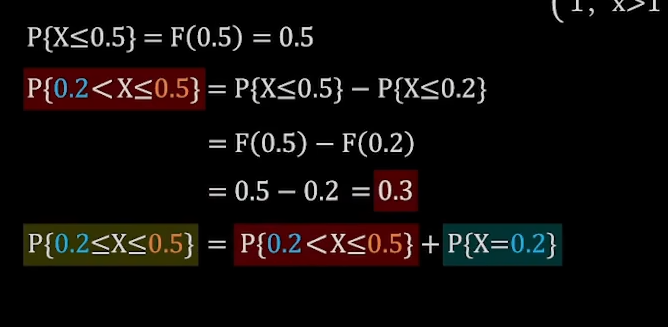
image.png

推论2

基于公式2
由
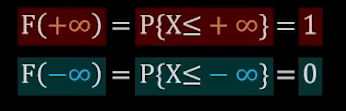
image.png
可得
image.png

例题4

image.png
前两个是推论，后面两个是条件

综合公式1和2

推论3：

image.png
image.png

推论4：

image.png
image.png

例题5

求积分，F-->f
image.png

例题6

求导数，f-->F
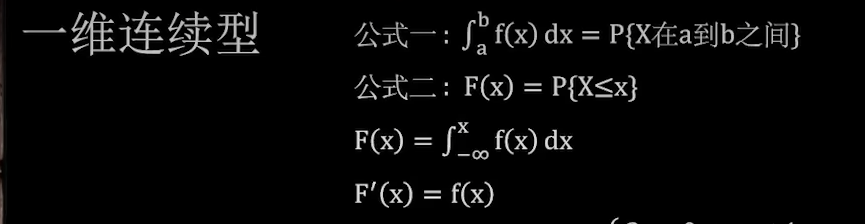
image.png

大综合公式

image.png
image.png

综合题目

FY(Y)的意思是P{Y<y}的意思
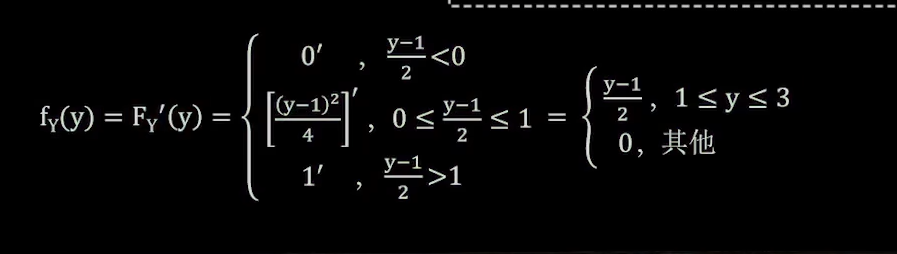
image.png
f求法
image.png

公式3

连续型求EX和DX
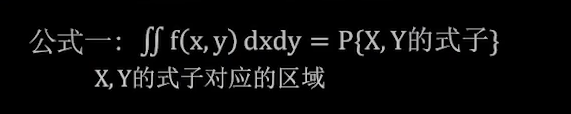
image.png

例8

image.png
image.png

二维连续型

image.png
image.png

推论1：

image.png
image.png

例2：

image.png
image.png

最难超级综合

前置公式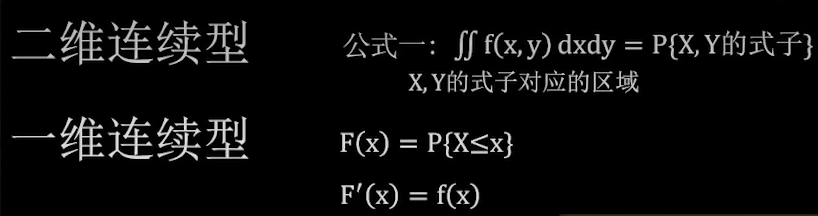
image.png

例3：

image.png
image.png

公式2

边缘概率密度
image.png

例题4：

image.png
image.png

公式3

独立性判断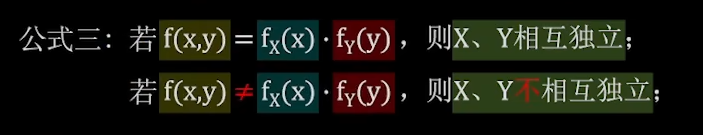
image.png

例5：

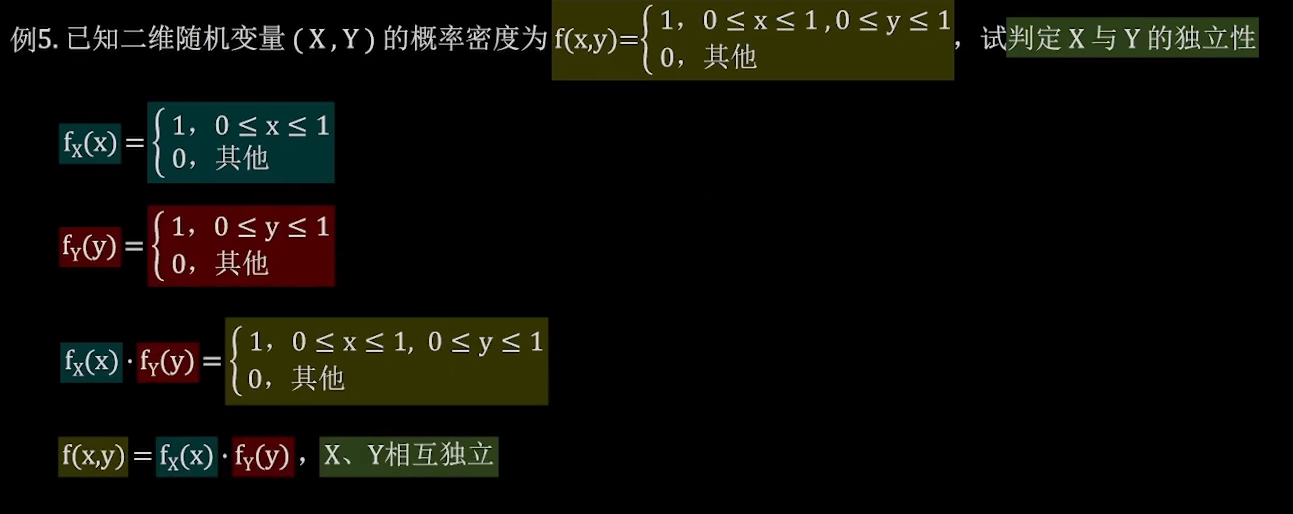
image.png
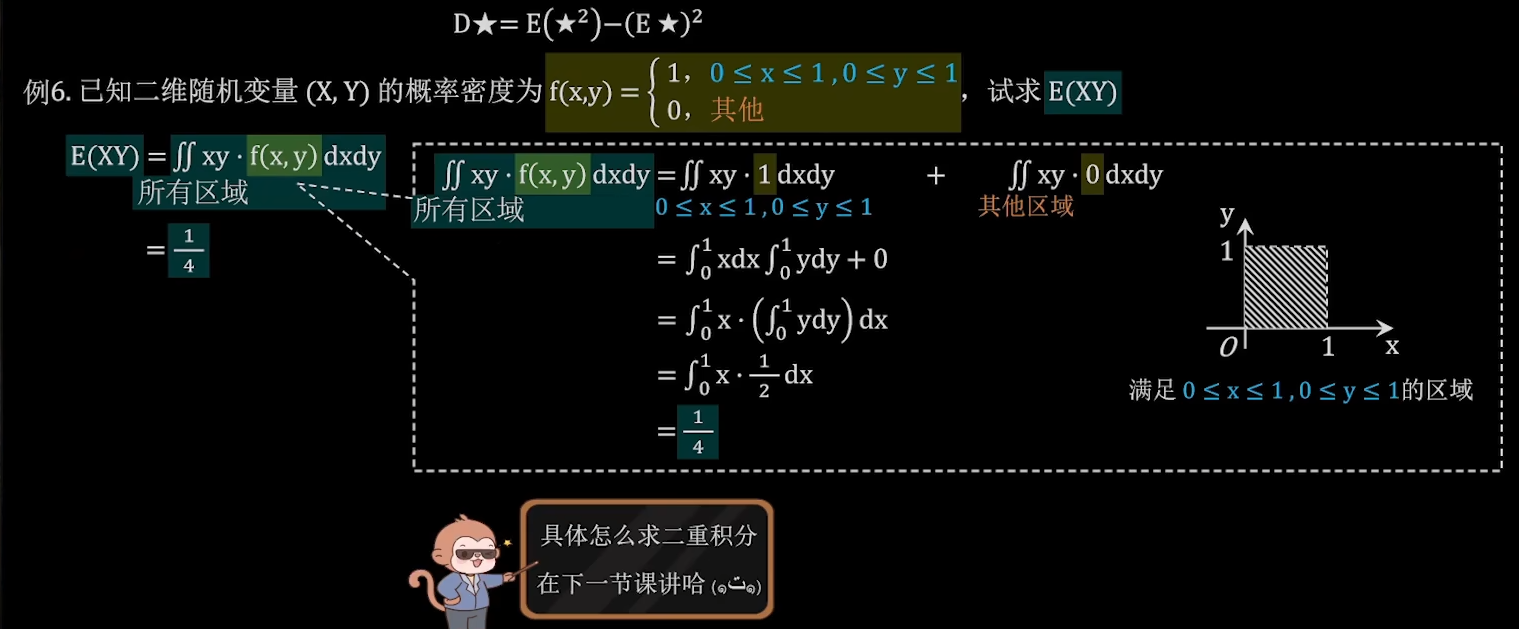
image.png

公式4

期望、方差
image.png

例6：

image.png
image.png

协方差

公式1

image.png
image.png

例题1：

离散
image.png
连续
image.png

公式2

XY是否相关
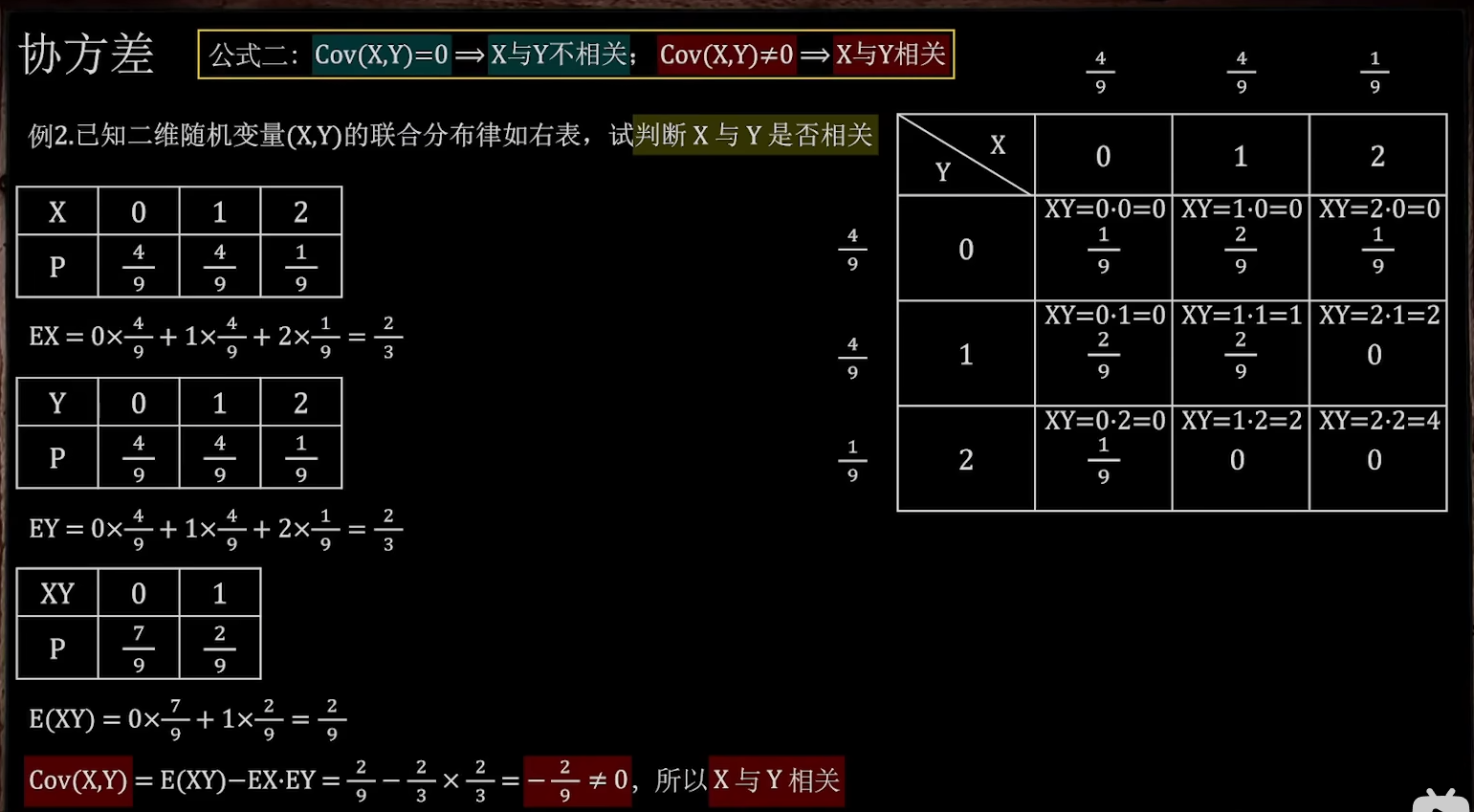
image.png

例2：

image.png
image.png

公式3

协方差相关系数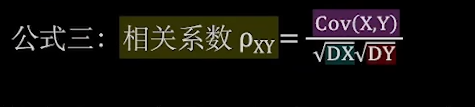
image.png
先求Cov(X,Y)再求方差
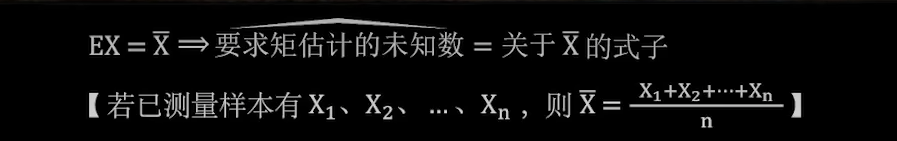
image.png

矩估计

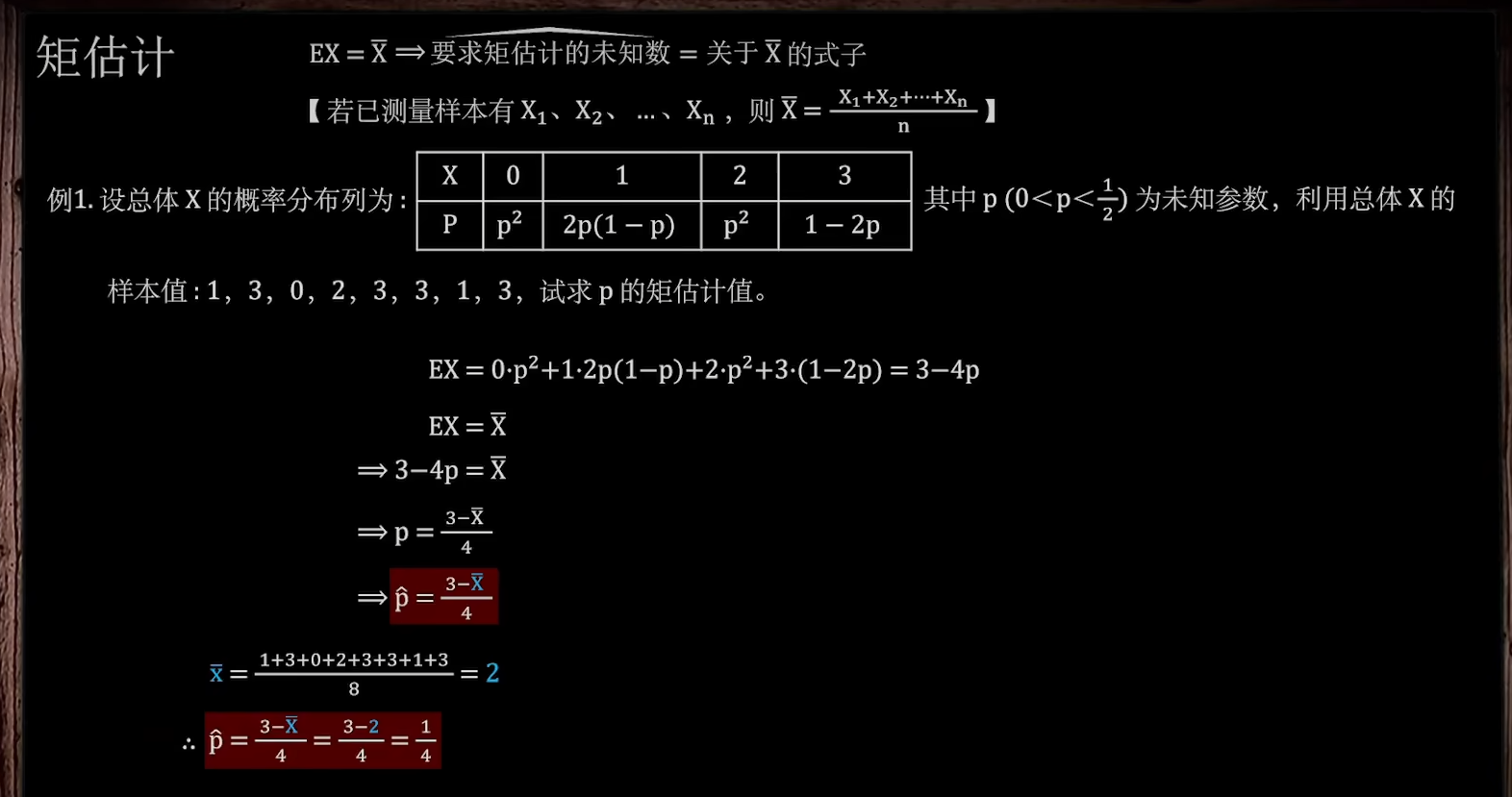
image.png
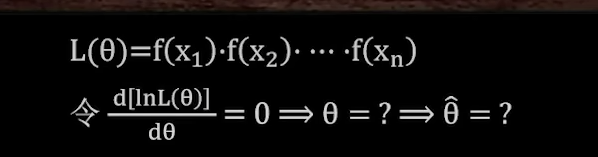
image.png

例1：
image.png

最大似然估计

image.png
image.png
image.png
image.png

题型

第二章

1. 比较难的古典概型，两次投骰子问题

image.png
把得到小的点数的事件分解为两种事件相加，第一种是两次都是一个数字，另外就是两次恰有一个此数字。
第一种无争议：1/6*1/6
第二种：先选一个最小数1/6，再选比次数大的任意数字，最后C12在两次投骰子中选取一次作为此数字，答案如图image.png

2. 已知概率密度求分布函数，即是已知f(x)求F(x)

易混淆点：
(1). 不能简单直接使用不定积分，这个需要以(-∞,x)为积分上下限进行定积分
(2). 由于所有分段区间都需要积分(-∞,x)区域，注意积分范围是否跨越需要计算的区域，则需要先对其范围积分出来，再与你所计算的区间的积分进行相加

image.png
image.png

3. 正态分布问题

记住公式与表格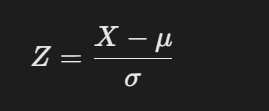image.png

image.png
image.png
image.png
image.png

image.png
概率的更多细节
image.png
一个分布函数F(Y)是另一个分布函数F(X)的函数，那么F(Y)可以由F(X)进行表示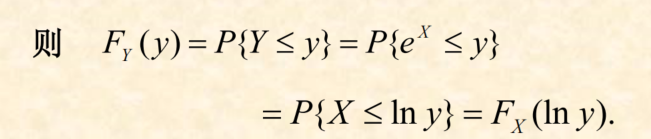image.png
答案：
image.png

小小知识点
image.png
image.png

偶函数对称积分区间，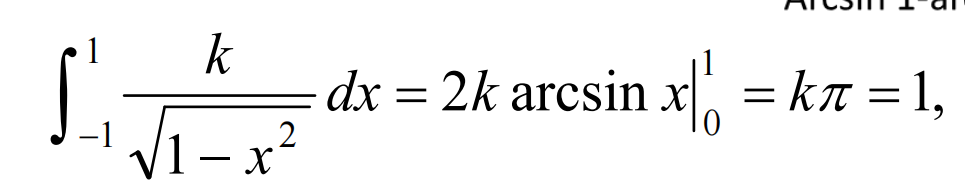
image.png
加一个x就是奇函数了，奇函数直接是0
另一题也用了同样的方法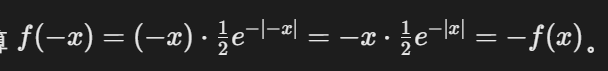image.png

第三章

1. 由概率密度花样求P

（1） 求概率P在规定X和Y或者只规定X或者Y的概率
image.png
（2）只规定X或者Y的概率，未规定的变量用定义域即可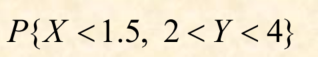
image.png
（3）以不等式规定的内层需要规定交换，外层为定义域，内层为交换后的关系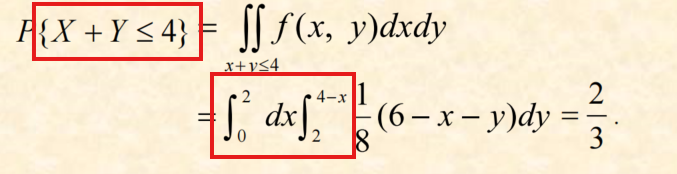
image.png

2. 求边缘分布律

image.png
分布函数 直接带入定义域即可，求谁谁就是未知数x或y，另外就是定义域

3. 求边缘分布律---边缘概率密度

image.png
求积分即可，注意积分范围需要结合xy两个定义域，综合写出
边缘概率密度的定义域结合原定义域画图写出来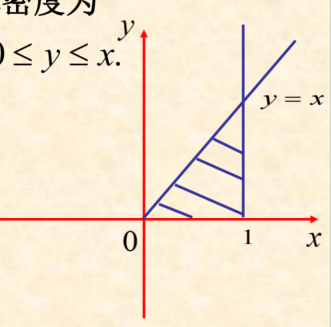image.png

4. 由单个边缘概率密度反求XY联合概率密度 image.png

小知识点：均匀分布意思如图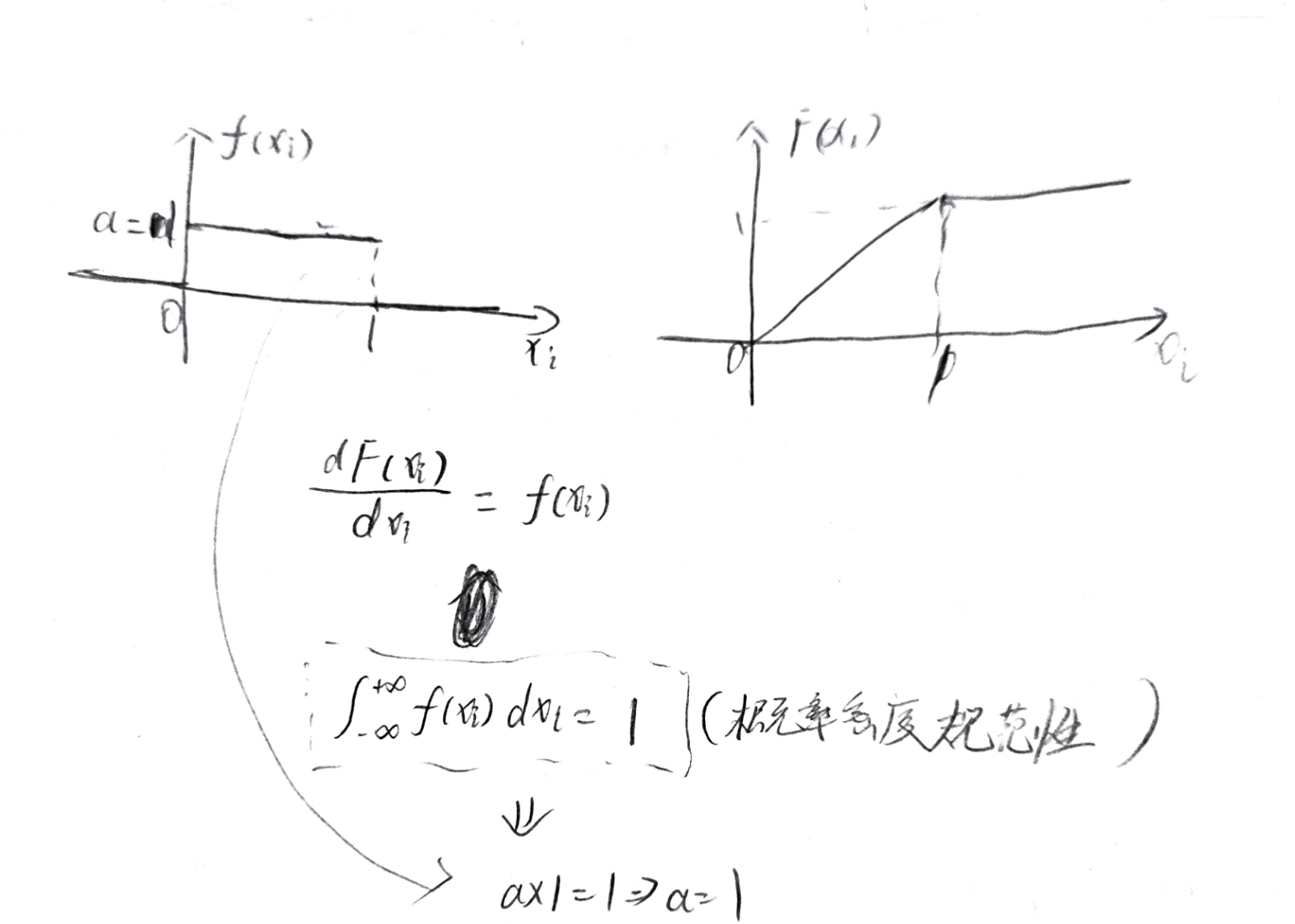image.png

例如：面积得1，然后连续均匀分布于0到1上

5. 卷积公式Z=X+Y

image.png
image.png
小知识点：

卷积公式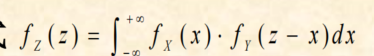
image.png
解答：
image.png

第四章

1. 随机变量分布律的期望存在问题

小知识点：数学期望对应的是绝对是收敛
image.png
image.png
image.png
image.png

2. 期望的实际问题

image.png
image.png

本题目主要不同在于，存在隐藏的第二个随机变量，两者仅联系在于：第一个的变量的0到1的概率，以及大于1的概率，作为第二个隐藏的离散型随机变量的概率，而题目目标在于第二个随机变量的期望的数值！
image.png

3. 实际问题2

小知识点：数学期望不可以进行非线性运算
image.png

小知识点：关于期望的原始公式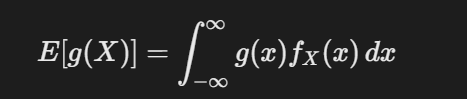image.png

其中g(x)是关键的，关于f(x)的函数，如果求原始的fx的期望直接赋值g(x)为x，如果要求关于f(x)函数的期望，则需要g(x)赋值为f(x)的函数，x设置为f(x)所代表的含义内容

小小知识点：立方差公式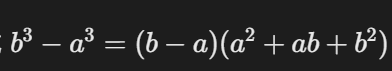image.png
小知识点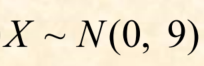：image.png

括号左边的数字代表期望EX，右边的代表方差DX

小知识点：DX运算的需要提出系数的平方到前面，如图

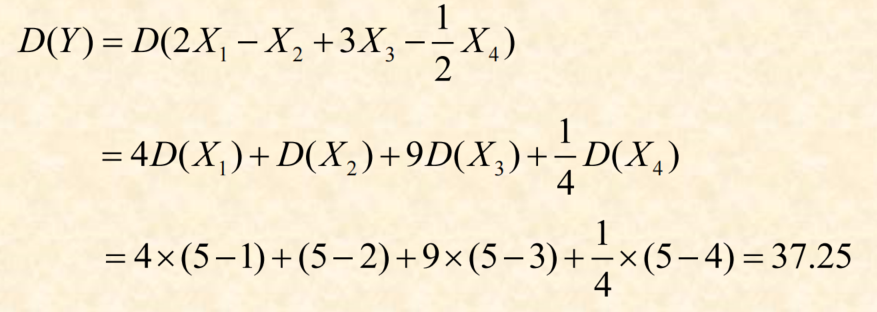
image.png
image.png

数理统计精讲

1. 求样本均值，样本方差，样本标准差

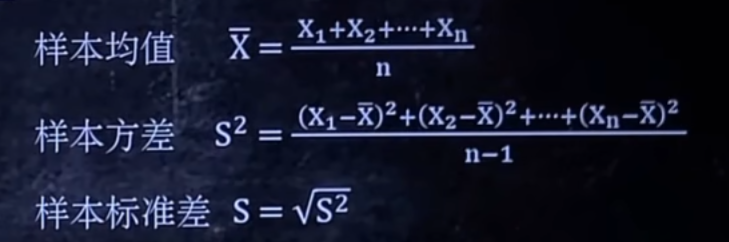
image.png
image.png

2. 求统计量的期望和方差

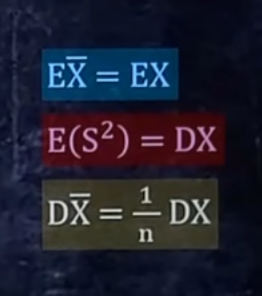
image.png
n为样本个数
泊松分布

参数为n，Ex和Dx就等于几

3. 三种分布

image.png
image.png
到底了:D
Copyright © 2025 fakeppa